Binary Trees
Binary Tree is a tree data structure in which each node has at most two children,left child and right child. Usually nodes in a tree can have multiple children but binary trees can have only two max. They are a useful data structure for storing data such as numbers and allow for fast lookup using binary search functionality.
the number of children each node has in a tree is called branching factor, and as such a binary tree has a branching factor of 2.
Similar to linked list a binary tree has a node which contains a value and a pointer to another node. But in a binary tree it has two pointers one for the left child and one for the right child.
class BST {
constructor(value) {
this.value = value;
this.left = null;
this.right = null;
}
}
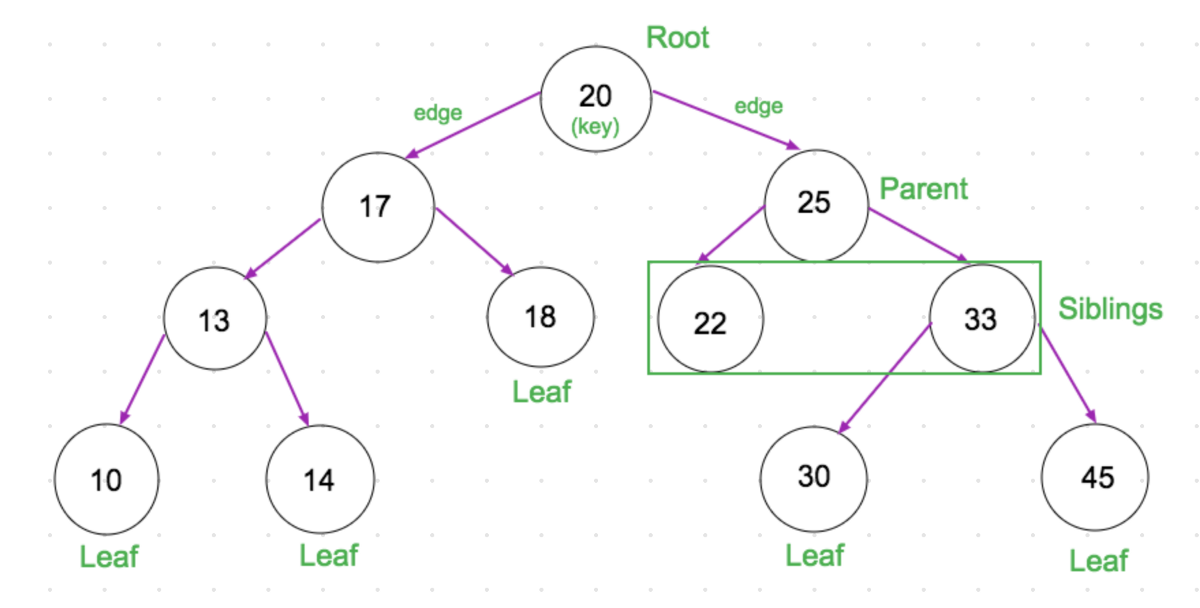
A binary tree uis made up of nodes and links/edges, The nodes represent the data stored in the tree, and the node at the top is called the root while every other node is a child node or a parent node. The nodes which point to no other node are called Leaf nodes. Nodes which have the same parent are called sibling nodes.
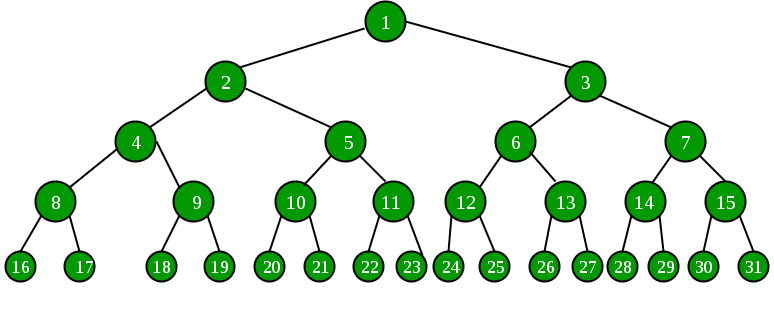
In general the number of nodes present in a tree will be one more than the number of edges/links present. Thus you can find the number of nodes present by counting the number of edges and adding one.
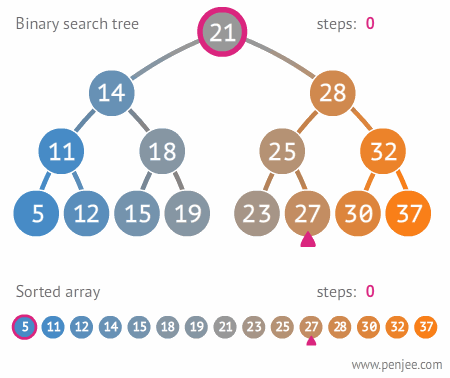
Below you can find how simple it is to search though a binary tree. https://blog.penjee.com/wp-content/uploads/2015/11/binary-search-tree-sorted-array-animation.gif
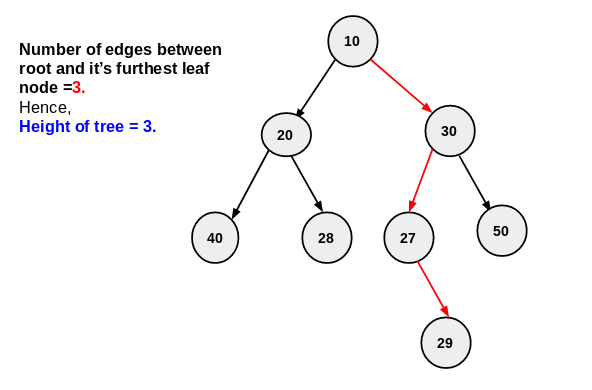
Another thing to pay attention for binary trees is the depth, node height, and tree height. To maximize efficiency of searching for an element in the tree.
We say that the depth of a node is the number of links from the root to the node. Thus the root node has a depth of zero and its direct children have a depth of 1.
We say that the height of a tree is the depth of the deepest node present in the tree from the root node. When we want to find a specific node height we look at the number of edges present from that node to a leaf node.
To find the maximum/larges number of nodes a binary tree can have we use this formula: 2^(height or n) - 1 max nodes possible at each tree height.
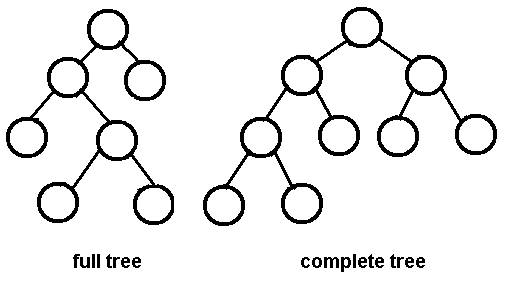
A given binary tree can be a full or complete binary tree. When we say a full binary tree we mean that each node has either exactly zero or two children. Since every node has to point to at least two nodes after the root node, a full binary tree cannot have an even number of nodes.
Whereas a complete binary tree is completely filled(except the last level sometimes) and is made so that all given sub nodes are as far left as possible.