Search Trees
Binary trees are used to store data so we want to have them be structured and sorted so that they are easy to search as previously stated. This is where Binary Search Trees(BST) come in, BST is a Binary tree where each node on the left(left subtree) has to contain smaller values and all nodes on the right(subtree) have to contain large values.
BSTs do not have any duplicate elements in the tree.
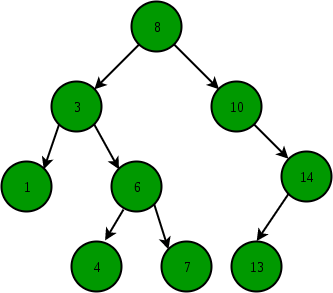
Following the given image above and using the rules stated above we can state that for example to insert 9 into the tree we can only do so as the left child of 10. 9 is greater than 8 so would have to go right side, we can't put it as a child of 13 as its a child of 14 which is greater than 10 thus all children of 14 have to be greater than 10.
So as an example for our BST above if we chose to implement the 4 traversal methods previously mentioned we would have the results shown below:
- BFS : [8,3,10,1,6,14,4,7,13]
- pre-order traversal : [8,3,1,6,4,7,10,14,13]
- in-order traversal: [1,3,4,6,7,8,10,13,14]
- post-order traversal : [1,4,7,6,3,13,14,10,8]
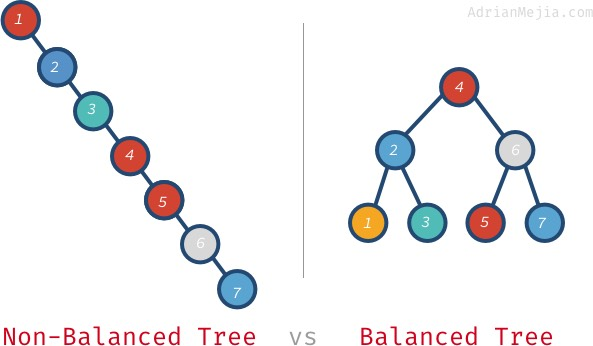
When working with BST if we want the best performance BST should be well balanced, so that both Branches are filled with no gaps. leaving a complete branch as previously stated.
We know that for any given BST that is complete/balanced, the time taken to find a given node is proportional to the node depth equal to approximately log2(n). therefore the runtime of this search will be of O(log n).
For an unbalanced tree the performance of the search is not as optimal as a balanced tree thus its runtime will be of O(n). Thus we can say that for a given tree its runtime will be between O(log n) and O(n) for best and worst case scenario. As can be seen in the picture below for an unbalanced tree we might have to traverse through all nodes present hence the run time of O(n).
One thing to make note of is that a balanced tree might not always be the best. For example if you're trying to see which has the best worst case for searches between a balanced tree with depth/height of 20 and unbalanced with 18. The best one in this case would be unbalanced with 18 as in the worst case only 19 comparisons will take place compared to the 21 required for the balanced tree.
But if you are searching for a particular value where both have the same number of nodes the best one would be an unbalanced tree.
When creating a BST to maintain the propoerties of BST each node inserted has only one correct position it could go in assuming each value inserted is unique. Thus the order in which numbers are added into the BST does affect the performance of the BST. Adding a sorted data into BST has the worst runtime of O(n).