Balancing
We know that a BST needs to be well balanced to give optimal performance and results, but there are different ways of balancing trees. Here
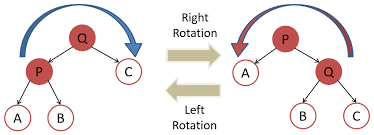
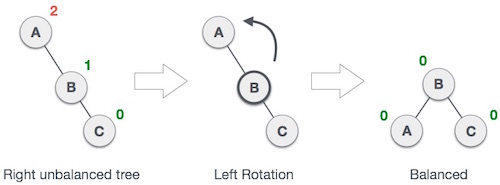
One way of balancing BSTs is a tree rotation, tree rotation changes the structure of the tree but does not affect the structure of the tree. Rotations are usually used to balance two branches of different depths.
In a rotation a node is shifted up while another node is shifted down. Other nodes may need to also be shifted to maintain the integrity of the binary tree. These rotations can change the height of the tree by moving large subtrees. As it can be seen below in both rotations the order of the nodes has not changed but the levels of the nodes has shifted.
We can also see that due to the rotation that the children of the nodes being rotated are also shifted but still stay the children of the nodes. Only thing changing the level/depth of these nodes. Thus we can see that this is a great way to balance trees as it does not matter if the node in rotation has parents. Hence we can use rotations at any level/depth within the tree.
In the example below you can see that we can use rotations to make a tree that is unbalanced balanced by applying rotations.
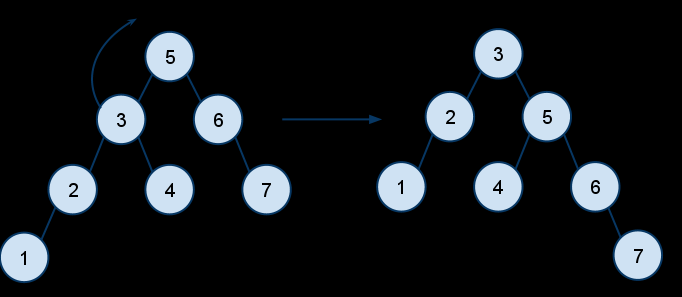
For the tree above after rotation has been applied the tree has been balanced. But balancing trees continually is not optimal hence AVL is applied.
AVL
AVL tree are a self balancing BST tree that applies rotation automatically as it's always balanced. Thus it is a much faster operation than most BSTs. When inserting a node the branch is inspected for balancing and the appropriate rotation is applied to make the tree balanced.
AVL looks at pattern of the branches in a tree where insertion of a node is occurring and looks for four patterns.
- Left-Left
- Left-Right
- Right-Left
- Right-Right
It performs these rotations after insertion of a new node, applying rotation to the node one or two levels above it or both.
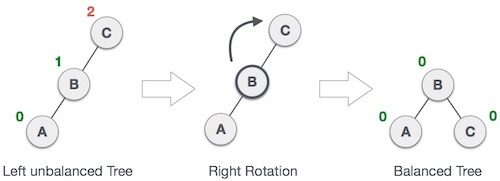
Left-Left(LL): In this operation a right rotation is performed on the node above the inserted node. As shown in the picture below the inserted node is moved up and the node two levels up is moved down.
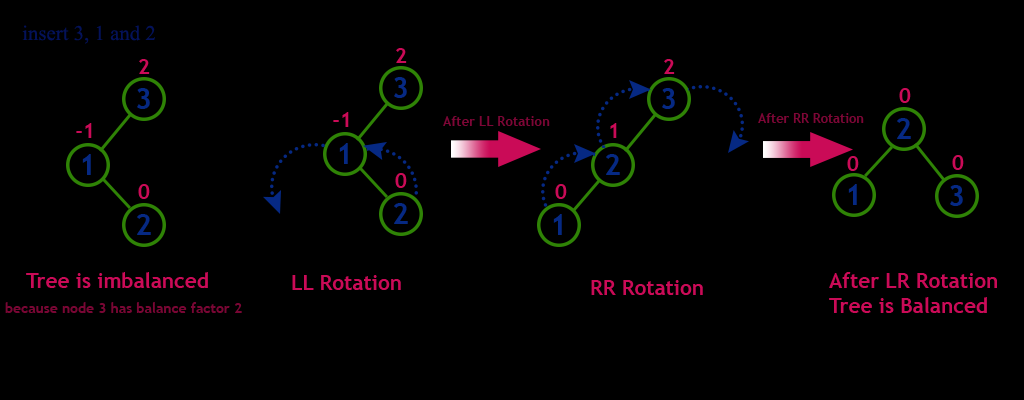
Left-Right(LR): This is a multi step process where a left rotation on the node above the inserted node is applied moving the above node down and the inserted node up. After which a right rotation is applied on the node that was two levels above the inserted node, moving the inserted node up and the top node down.
Right-Left(RL): In this operation a right rotation is performed on the node above the inserted node moving the inserted node up and the above node down. After that a left rotation is performed on the node two that was above two levels the inserted node. moving the above node below the inserted node.
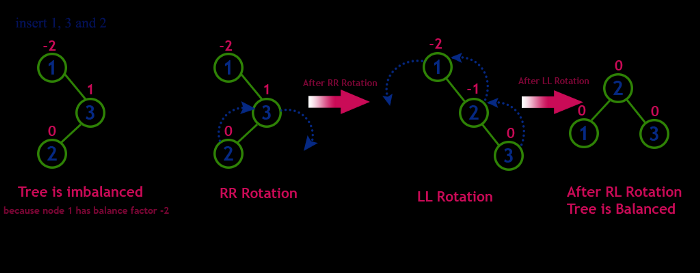
Right-Right(RR): In this operation a left rotation is performed on the node above the inserted node, moving it up and the node two levels up down.
As can be seen thus far balancing is really easy with AVL trees, But the downsides of AVL is insertion and deletions. In these cases they can be operationally heavy as several rotations per each operation can be required.
RED-Black
There is another self balancing tree similar to AVL, the red-black tree. This algorithm does not have strict balancing requirements like AVL so its look up is slower than AVL, but its insertion and deletion operation are much faster due to requiring less rotations per operation.
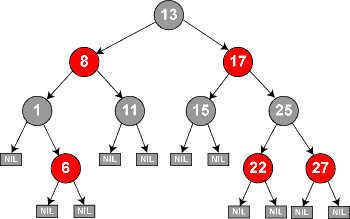
How these trees work is that each node in the tree is either red or black, where new inserted nodes are always marked red. After insertion the color of the surrounding nodes is assessed and the nodes are rotated or repainted to achieve the conditions below:
- All red leaves must have only child nodes colored black.
- the root of the tree must always be black
- No matter where you are in the tree, every path to a leave/leaf node must go through the same number of black nodes.
The tree resulting from this algorithm is not perfectly balanced as AVL trees but its runtime operation for lookup is still O(log n) and for insertion and deletion.
This is due to the tree having a maximum total height of 2 log (n+1)
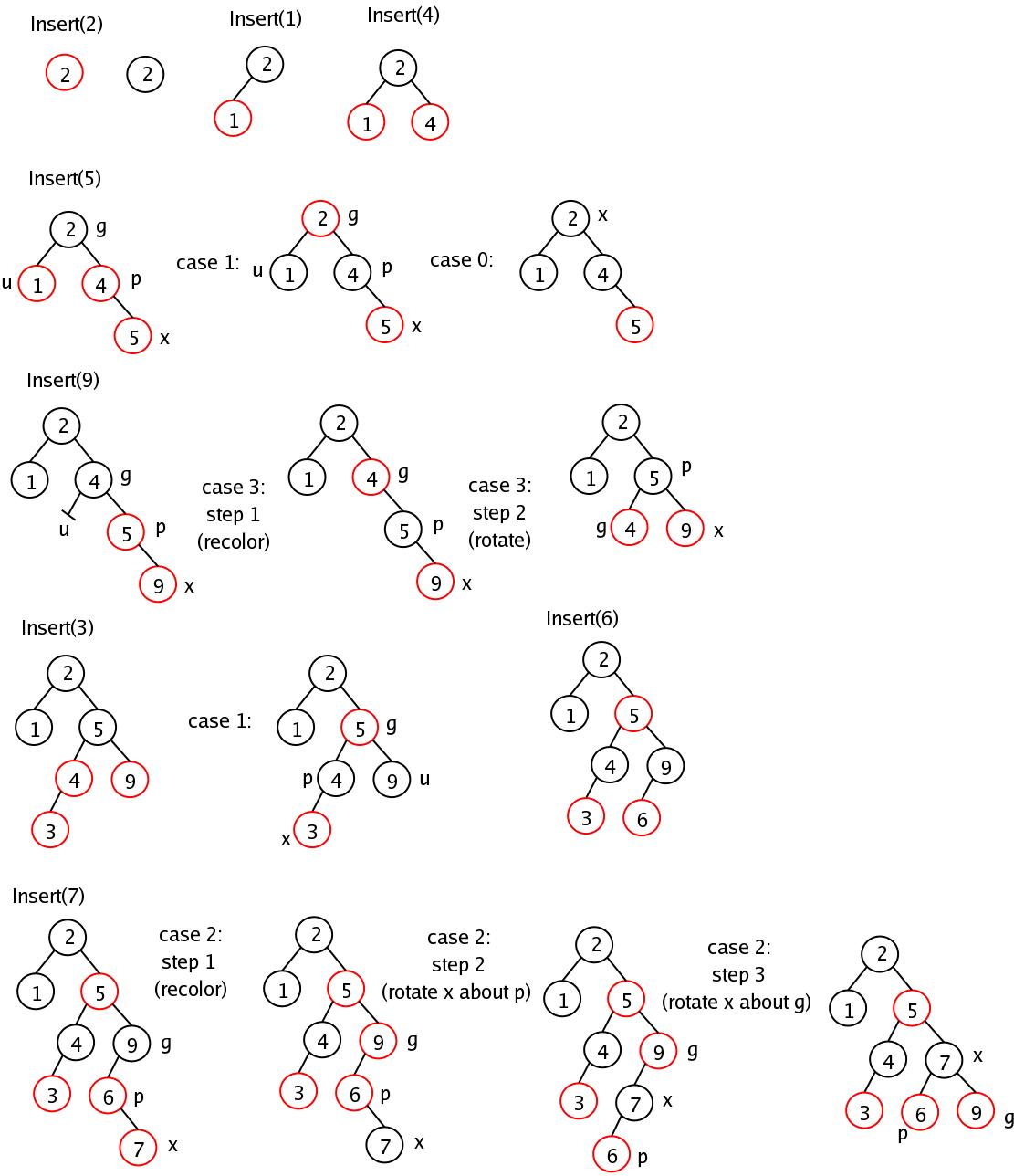
Insertion
When a new node is inserted into a red-black tree, the algorithm searches through the tree to find the correct spot based on the value and places the node(similar to BST) then paints the node red. After that is complete it assesses the surrounding nodes and performs either of these 4 actions:
-
In the first case the new nodes parent is black, the red-black properties are upheld and nothing is done.
-
The second case the new nodes parent and its siblings are painted red. Here you would switch the color of the parent and parent sibling node to black and switch the grandparent to the node to red.
-
Here the new nodes parent is red and its sibling is black, and the new nodes value is between the parent and grandparent.
- If the new node is greater than the parent, the parent is rotated left, where as if the node is less than the parent the parent is rotated right.
-
The last case is where the new nodes parent is red and the parent sibling is black. The parent node should be between the value of the new node and the grandparent.
- If the new node value is less than the parent, the grandparent is rotated right and the colors of the parent and grandparent are swapped.
- if the new node value is greater than the parent, the grandparent is rotated left and the colors are swapped.
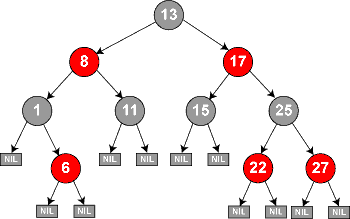
For the tree below if we were to insert 7, based on rules of BST it will be inserted in the right branch of 6. After which we would follow the cases outlined above, The grandparent (1) is rotated left and the colors of grandparent and parent nodes and it's children are switched.
Another example:
In general AVL and red-black trees will have a faster runtime for lookup compared to BST and binary tree.
Thus we can say that if a runtime of a algorithm for lookup is closer to O(N) we know that it will not be AVL or red-black trees as their lookup time is guaranteed to be in O(log n).
When looking at creating a tree and if we're choosing between AVL and red-black, we look and see if we will be doing lots of insertion and deletion operations if so the best bet is to go with red-black trees. But if the tree is static or unchanging the best tree to use would be AVL.