Graphs

A structure like this is called a graph, and the points W,E,S,N would be called vertices and the lines connecting them can be represented as edges.

A lot of things can be implemented as a graph such as a road network where intersections can be vertices and the road as edges. Graphs are how most GPS devices work.

If you travel through all the edges once, you'd call the eulerian path, eulerian path is one that uses every edge exactly once and the number of vertices passed does not matter. The eulerian path starts or ends at the vertex, one of the ways to recognize the start and end of a path is by looking at vertices which has an odd number of edges. That means it is one of the two ends of the eulerian path. Thus by that logic we can say that if a graph has more than two vertices with odd edges, there is no eulerian path.

Another image example of graphs can be found below. Which shows how graphs can either be directed or undirected graph. The only difference between both graphs is one has directionality, So for example in the directed graph if you are 1 you can only travel towards 2, as you have to observe and follow the directionality of the graph. where as in the undirected graph we can travel to 0,2,and 4 from 1.

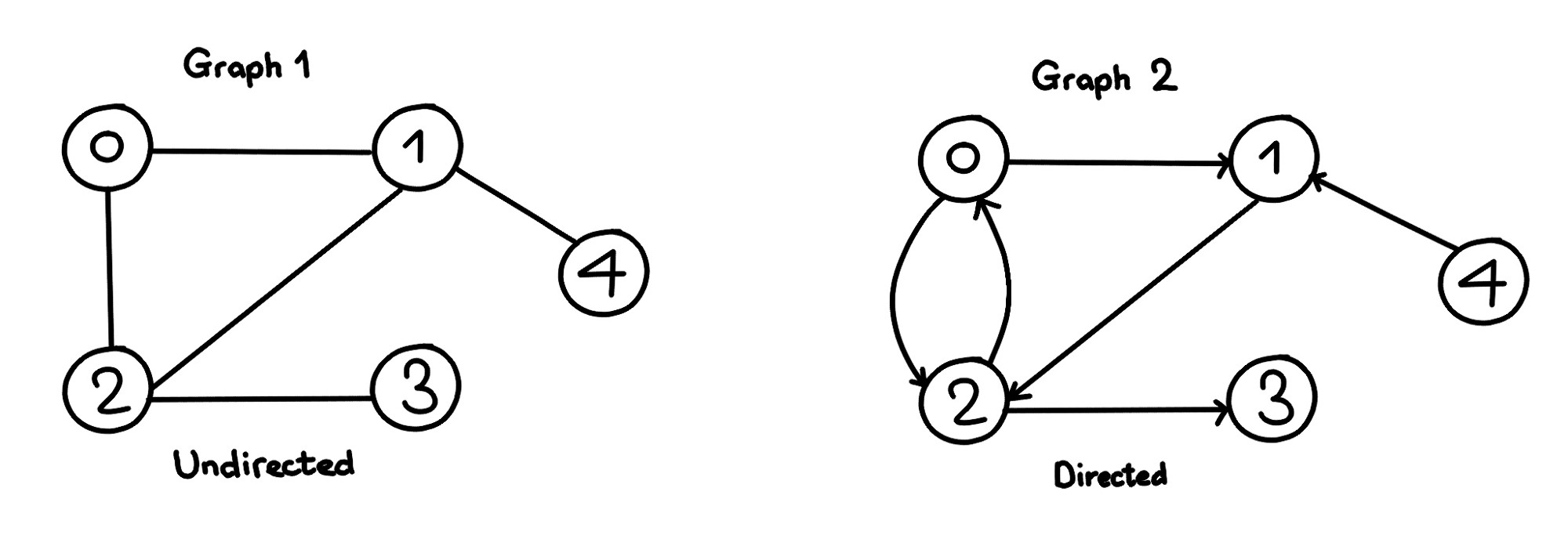
One useful terminology is considering the connected edges of a given node as neighbor nodes. Though this has to follow the directionality of the graph. So if we look at our example graph above. We can say that for the node 1, it's neighbor is 2, for node 0 it's neighbor is 2 and 1.

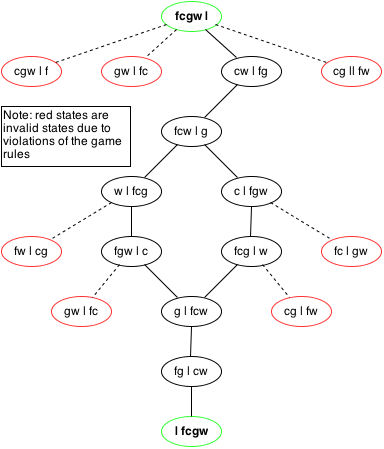
Graphs can also be created to solve and represent puzzle games Such as the farmers problem where the farmer has to get a wolf a goat and cabbage across the river, but the boat they have has only room for one more item.

This can be represented by a graph as such where each possible state is mapped out including the ones that break the rules of the game. Where the moves made are edges and the arrangement of the items and farmer are vertices.

As there is 4 characters and three locations we can say that there are 3^4 possible states including invalid moves for the problem:

Backlinks

Children

Traverse